MATRICES DE ECUACIONES LINEALES CON 3 INCOGNITAS

 En esta  matriz se trata de encontrar el valor de x, y, z

Para eso el primer paso es: convertir los tres números de la parte izquierda a 0, es decir multiplicar fila por fila y sumar o restar según sea lo conveniente






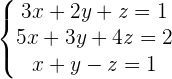
El método de Gauss consiste en utilizar el método de reducción de manera que en cada ecuación tengamos una incógnita menos que en la ecuación precedente. Tomando el sistema siguiente, lo vamos a resolver paso por paso usando el método de Gauss

1 Ponemos como primera ecuación la que tenga como coeficiente de :  ó , en caso de que no fuera posible lo haremos con  o , cambiando el orden de las incógnitas.

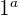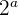2 Hacemos reducción con la  y  ecuación, para eliminar el término en  de la 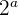 ecuación. Después ponemos como segunda ecuación el resultado de la operación:

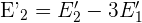
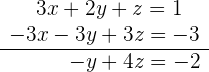
3 Hacemos lo mismo con la ecuación 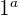 y  ecuación, para eliminar el término en .

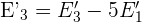
4 Tomamos las ecuaciones 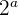 y , trasformadas, para hacer reducción y eliminar el término en .

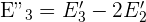
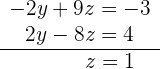
5 Obtenemos el sistema equivalente escalonado.

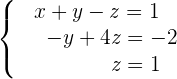
6 Encontramos las soluciones.

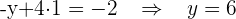
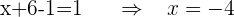
Referencias:

https://www.superprof.es/apuntes/escolar/matematicas/algebra/ecuaciones/sistema-de-tres-ecuaciones-con-tres-incognitas.html

https://www.youtube.com/watch?v=XRcx8-2lLJI&t=901s

https://www.ecured.cu/Sistemas_lineales_de_tres_ecuaciones




Comentarios

Publicar un comentario

Entradas más populares de este blog

REGLAS DE DERIVACION

Imagen
 Cuando es constate siempre vale =0 Cuando es solo X = 1 La siguiente regla es la de dx =nx -1    y = a x al cuadrado n= 2  y'=2x Cuando es una fracción  se mueve a nuestra conveniencia para poder derivarlo cuando es negativo o fracción tenemos que pasarlo a positivo y después convertirlo en raíz. la 5ta regla de derivación  primero buscamos u y v después operamos du *v + dv*u ahora   si sacamos la respuesta. es importante tener los pasos bien claros y diferenciar u y v. Las reglas de derivación son fórmulas que se utilizan para calcular la derivada de una función.   Reglas básicas La derivada de una suma de funciones es igual a la suma de sus derivadas.   La derivada de una diferencia de funciones es igual a la diferencia de sus derivadas.   La derivada de una función constante es cero.   La derivada de un producto de dos funciones es igual a la suma de dos productos.   Regla de los cuatro pasos   Se determina f (x +...
Leer más

LIMITES TRIGONOMETRICOS

Imagen
 Estos son los mas difíciles que se me hicieron por la sustitución y cuando aplicarlo. Límites trigonométricos Los límites trigonométricos son una parte fundamental del cálculo y desempeñan un papel crucial en entender el comportamiento de las funciones trigonométricas a medida que se acercan a ciertos valores. Estos límites son esenciales en el análisis matemático y son utilizados en diversas ramas de la ciencia y la ingeniería. Para comprenderlos a fondo, es necesario explorar los conceptos clave asociados con las funciones trigonométricas y cómo se comportan en situaciones límite. Límites trigonométricos Se le denomina limites trigonométricos a los límites que contienen funciones trigonométricas como por ejemplo: Sen(x), Cos(x), Tag(x), entre otras. Para la resolución de estos límites se recomienda evaluar primero, dado un resultado directo, pero en aquellos casos que presenten alguna indeterminación se recomienda aplicar las consideraciones según sea  ,  , 0.∞, ∞-∞,...
Leer más

SEGUNDO PARCIAL;DERIVADA DE UNA FUNSION

Imagen
Yo entendí aquí que a cada x se le agrega y así es x+h y se le resta la fusión principal ,también usamos el binomio y de allí operamos podemos hacer el binomio largo o corto multiplicando ,en fracción  hacemos el sándwiches y en raíz aplicamos el conjugado espero recordar todos los pasos por que son muchos pero como dijo es para ver de donde sale el resultado.. Más información ¿Sabías que...? Cociente incremental Derivadas sucesivas Derivada de una función El concepto de derivada de una función matemática se halla íntimamente relacionado con la noción de límite. Así, la derivada se entiende como la variación que experimenta la función de forma instantánea, es decir, entre cada dos puntos de su dominio suficientemente próximos entre sí. La idea de instantaneidad que transmite la derivada posee múltiples aplicaciones en la descripción de los fenómenos científicos, tanto naturales como sociales. Variación de una función Dada una  función  f (x), se define  variación de ...
Leer más