MATRIZ TRANSPUESTA
la matriz transpuesta es cambiar filas por columnas es decir si tienes una matriz de 3x2
te quedara una matriz de 2x3...
2 -5 2 6 -3
6 7 -5 7 5
-3 5
Definición y propiedades de la matriz traspuesta.
La mayor aplicación práctica de la matriz traspuesta es el cálculo de la matriz inversa.
Definición informal
La matriz traspuesta de una matriz se denota por y se obtiene cambiando sus filas por columnas (o viceversa).
Ejemplo:
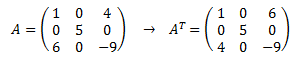
Obsérvese, por ejemplo, que la primera fila de la matriz A es (1,0,4). Esta fila es la primera columna de su matriz traspuesta.
Obsérvese, por ejemplo, que la primera fila de la matriz A es (1,0,4). Esta fila es la primera columna de su matriz traspuesta.
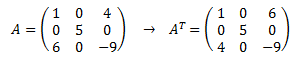
Obsérvese, por ejemplo, que la primera fila de la matriz A es (1,0,4). Esta fila es la primera columna de su matriz traspuesta.
Obsérvese, por ejemplo, que la primera fila de la matriz A es (1,0,4). Esta fila es la primera columna de su matriz traspuesta.Definición formal
Sea A una matriz de dimensión mxn, denotamos al elemento de la fila i y columna j como A(i,j), siendo i<m y j<n.
Entonces, se define la matriz traspuesta de A como la matriz de dimensión nxm tal que , siendo i<m y j<n.
Propiedades de la matriz traspuesta
- Traspuesta de la traspuesta
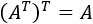
- Traspuesta de la suma
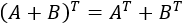
- Traspuesta del producto
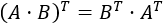
- Una matriz es igual que su traspuesta si, y sólo si, es simétrica
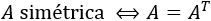
- El determinante de una matriz regular es igual al de su traspuesta
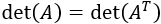
- Si A es regular, su inversa es la transpuesta de su matriz adjunta (Adj(A)) entre su determinante:
REFERENCIAS//
https://www.geogebra.org/m/mafmgjpd#:~:text=La%20matriz%20traspuesta%20de%20una,columna%20de%20su%20matriz%20traspuesta.
https://www.youtube.com/watch?v=aTsgBk34zyY&t=125s

Comentarios
Publicar un comentario